最近在学javaweb, 把自己博客给忘得差不多了，于是水篇文章证明我还活着()
DFS(深度优先搜索)
概述
深度优先搜索 (Depth-first-search) 是一种图的算法, 以深度作为方向进行搜索,找到所需要的答案, 直到所有方案搜索完为止，其本质依然是暴力。
走入迷宫, 向一条路径一直走下去直到走到死路为止, 再回返到最近的一个路口走另一条没有走过的路，依次类推…
实现dfs的核心是标记与回溯。
模版
void dfs(int x){
if(满足停止搜索条件){
... //处理
return;
}
for (int i = 0; i < length; i++){
if (没有搜过该点){
vis[x] = 1; //标记搜过
dfs(x + 1); //递归
vis[x] = 0; //取消标记(回溯)
}
}
}
dfs变化多样,不一定就要照着模版写。
题目尝试
C语言新手, 请多多指教。
CF6A Triangle
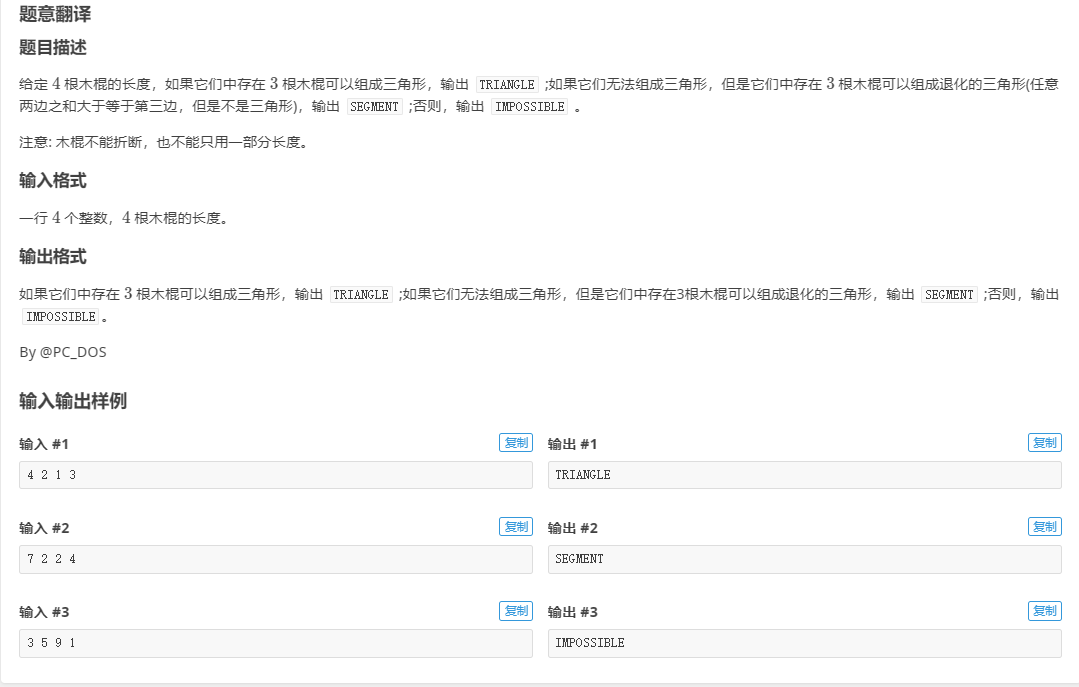这是一道入门题, 数据少也不卡时间, 可以直接通过暴力枚举得到结果简单方便, 但还是用dfs来练练手()我们可以先将所有木棍从小到大排序,当我们任意取出3根木棍时，这3根木棍的长度一定是有序的,判断三角形时只需要将1、2号木棍与3号木棍长度进行比较即可。
AC代码:
#include<stdio.h>
#include<bits/stdc++.h>
using namespace std;
//直接调用C++的sort排序，懒得写排序了。
//arr进行数据读入，arr1放入需判断的三根木棍, con代表状态。
int arr[4], arr1[4], i, con = 0;
void dfs(int cur, int w)//cur代表已读入木棍数，该值等于3则开始判断三角形情况。
{
if (cur == 3)
{
//大于为三角形，等于为退化三角形
if(arr1[0] + arr1[1] > arr1[2])
{
con = 1;
}
else if (con == 0 && arr1[0] + arr1[1] == arr1[2]) //为什么要判断con==0呢
{
con = 2;
}
}
else
{
/*
w表示当前搜索到的位置
我们从头开始理,最开始主程序调用dfs时:
1.w = 0, cur = 0, 会进入到这里，j = 0开始循环, arr1放入0号元素, 递归;
2.w = 1, cur = 1, 依然进入到这里, j = 1开始循环, arr1放入1号元素, 递归;
3.w = 2, cur = 2, 依然进入到这里, j = 2开始循环, arr1放入2号元素, 递归;
4.cur = 3, 判断条件，这里结束后将返回到第3步;
5.第3步此时位于j = 2的循环中，dfs结束后，j++后变为3, arr1将不再放入2号元素而是放入3号元素，递归;
6.cur = 3, 判断条件，这里结束后将返回到第3步;
7.第3步到达循环末尾，再回到第2步,第2步j++后变为2,取3号元素，以此类推...
8.你应该能理解为什么要写循环了。
*/
for (int j = w; j < 4; j++)
{
arr1[cur] = arr[j]; //放入arr1数组
dfs(cur + 1, j + 1); //当前数量+1并递归搜索
}
}
}
int main(void)
{
for (i = 0; i < 4; i++)
{
scanf("%d", &arr[i]);
}
sort(arr, arr + 4); //快排
dfs(0,0); //dfs开始搜索
if (con == 1)
{
printf("TRIANGLE");
}
else if (con == 0)
{
printf("IMPOSSIBLE");
}
else
{
printf("SEGMENT");
}
}
CF629A Far Relative’s Birthday Cake
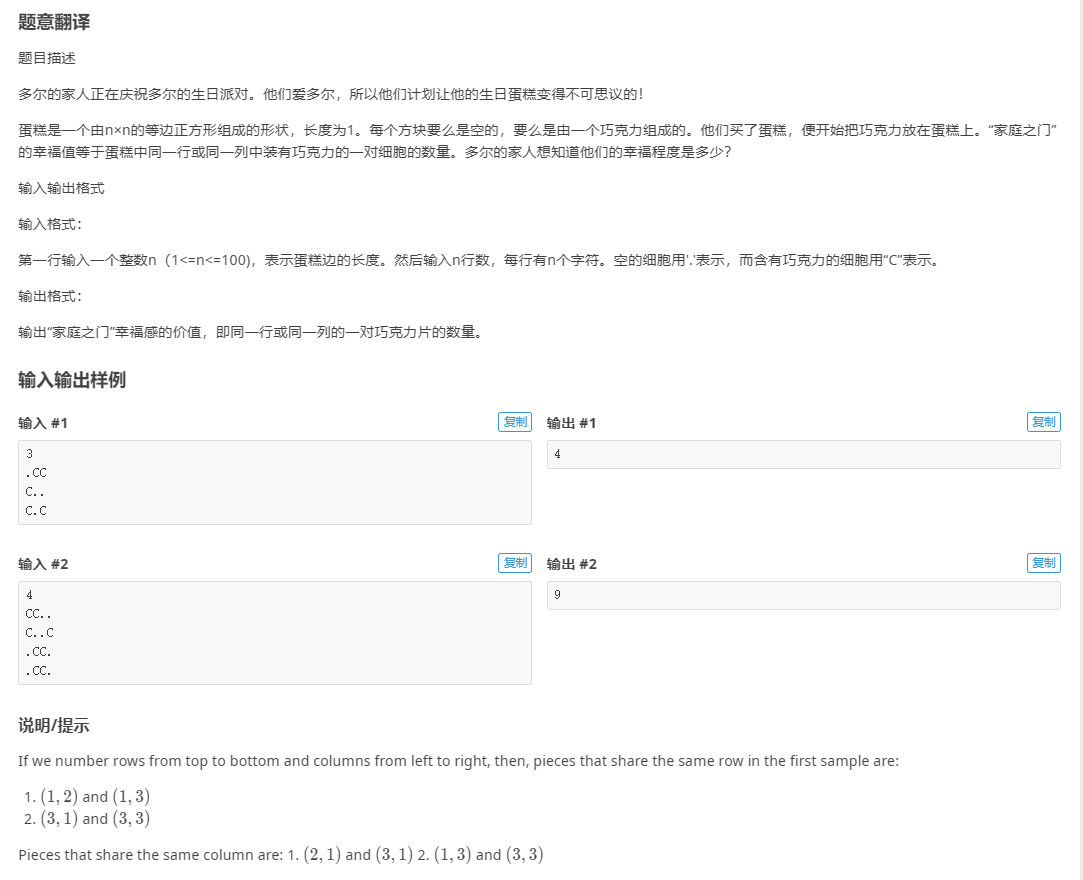解释解释到底说了什么：只要在一行或一列上找到一对CC,就得到一点幸福指数，求总幸福指数。我们使用dfs进行搜索时带上一个数组arr1,用它来标记是否搜索过该元素,递归完成后取消标记,这就是标记与回溯。
AC代码:
#include<stdio.h>
const int MAX = 110;
int n, arr[MAX][MAX] = {0}, arr1[MAX][MAX], count = 0, i, j;
void dfs(int a, int b){
//判断条件:x轴上的b小于n或y轴上的a小于n
if ((a == i && b < n) || (b == j && a < n))
{
if (arr[a][b] == 1 && arr1[a][b] != 1)
{
//标记解
count++;
}
//往下和右递归调用
dfs(a+1, b);
dfs(a,b+1);
}
}
int main(void)
{
//读入,将str数组转化为arr数组
scanf("%d\n", &n);
for (i = 0; i < n; i++)
{
for (j = 0; j < n; j++)
{
char temp;
scanf("%c", &temp);
if (temp == 'C')
{
arr[i][j] = 1;
}
else if (temp == '.'){
arr[i][j] = 0;
}
}
if (i != n - 1)
{
scanf("\n");
}
}
//只是把dfs的循环拿出来用了，原理一致。
for (i = 0; i < n; i++)
{
for (j = 0; j < n; j++)
{
if (arr[i][j] == 1)
{
//标记与回溯
arr1[i][j] = 1;
dfs(i, j);
arr1[i][j] = 0;
}
}
}
printf("%d", count);
}
P1706 全排列问题
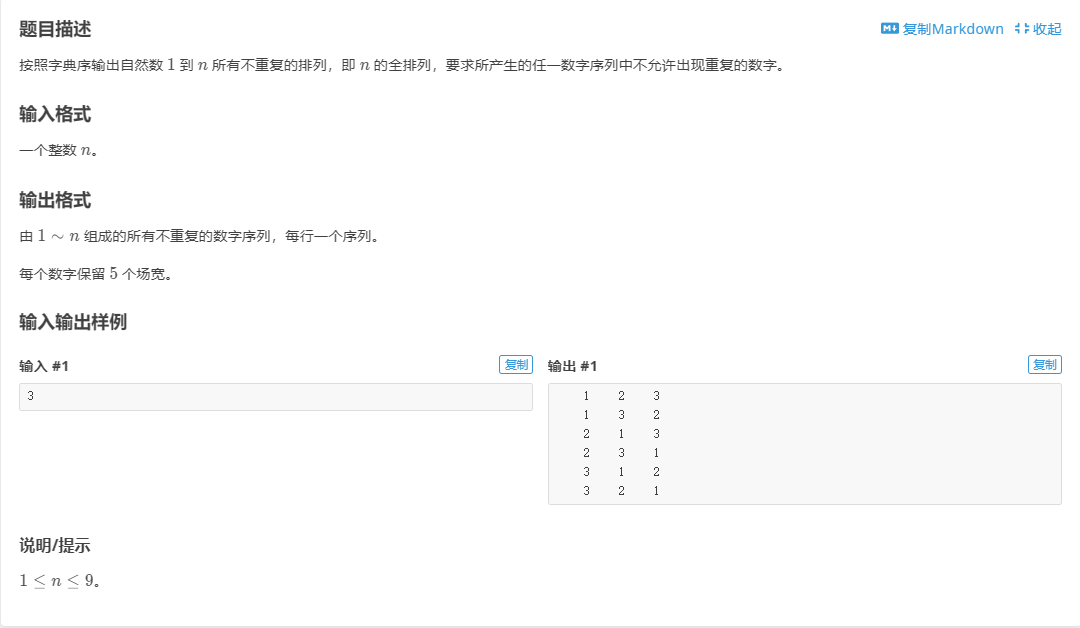经典题,与上题思想一致,使用dfs深度搜索,用另一个数组去标记是否搜索过该数。与第一道题不同, 我们所搜索的元素只可能在当前位置之后, 所以直接从当前位置循环, 而此题的排列没有任何顺序可言,我们从数组中遍历没有被标记的元素来作为下一个应该排的位置,所以区别还是挺大的()
AC代码:
#include<stdio.h>
int a[10], v[10], n;
void dfs(int t){
if (t == n + 1)
{
for (int i = 1; i <= n; i++)
{
printf(" %d", a[i]);
}
printf("\n");
return;
}
for (int i = 1; i <= n; i++)
{
if(v[i] != 1)
{
v[i] = 1;
a[t] = i;
dfs(t + 1);
v[i] = 0;
}
}
}
int main(void)
{
scanf("%d", &n);
dfs(1);
}
P1451 求细胞数量
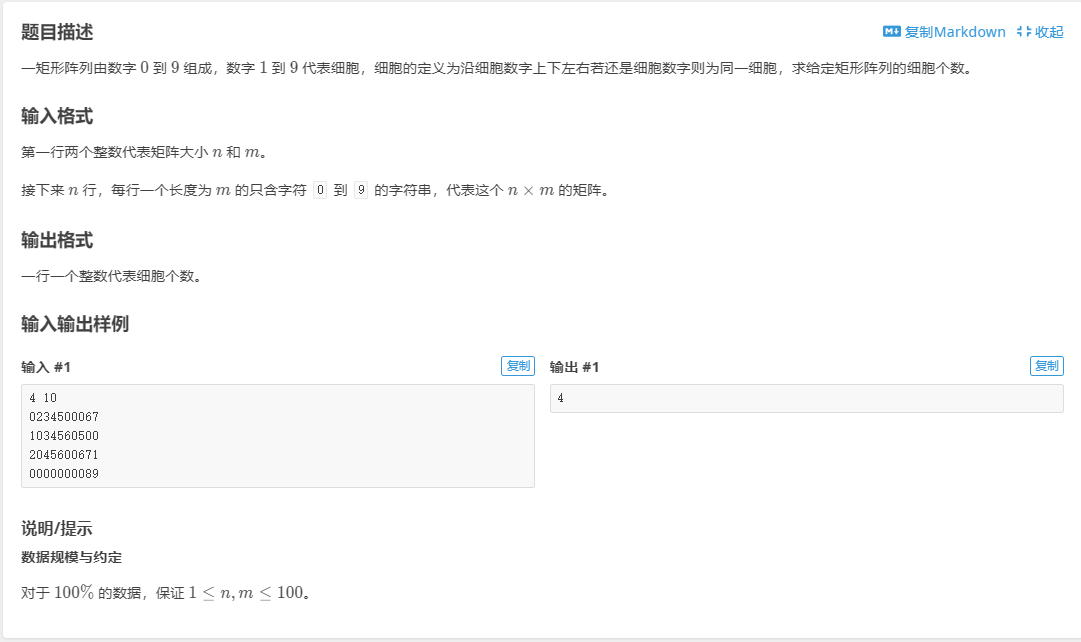连通块问题,只要连通的区域统统都算1个,直接dfs,将要搜索的设为1,dfs搜索到的区域统统变为0,注意递归时是朝东南西北四个方向进行搜索, 当触碰到边界时停止搜索。AC代码:
#include<stdio.h>
const int MAX = 110;
int m, n;
int arr[MAX][MAX];
int count = 0;
//方向数组,分别对应东南西北。
int dx[4] = {0,0,1,-1};
int dy[4] = {1,-1,0,0};
void dfs(int a, int b)
{
arr[a][b] = 0;
for (int i = 0; i < 4; i++)
{
a += dx[i];
b += dy[i];
//判断搜索条件
if (a <= m && a >= 1 && b <= n && b >= 1 && arr[a][b] == 1)
{
dfs(a, b);
}
a -= dx[i];
b -= dy[i];
}
}
int main(void)
{
scanf("%d%d\n",&m,&n);
char temp;
for (int i = 1; i <= m; i++)
{
for (int j = 1; j <= n; j++)
{
scanf("%c", &temp);
if (temp <= '9' && temp > '0')
{
arr[i][j] = 1;
}
else
{
arr[i][j] = 0;
}
}
if (i != m)
{
scanf("\n");
}
}
for (int i = 1; i <= m; i++)
{
for (int j = 1; j <= n; j++)
{
if (arr[i][j] == 1)
{
dfs(i, j);
//得到其一解
++count;
}
}
}
printf("%d", count);
}
P1506 拯救oibh总部
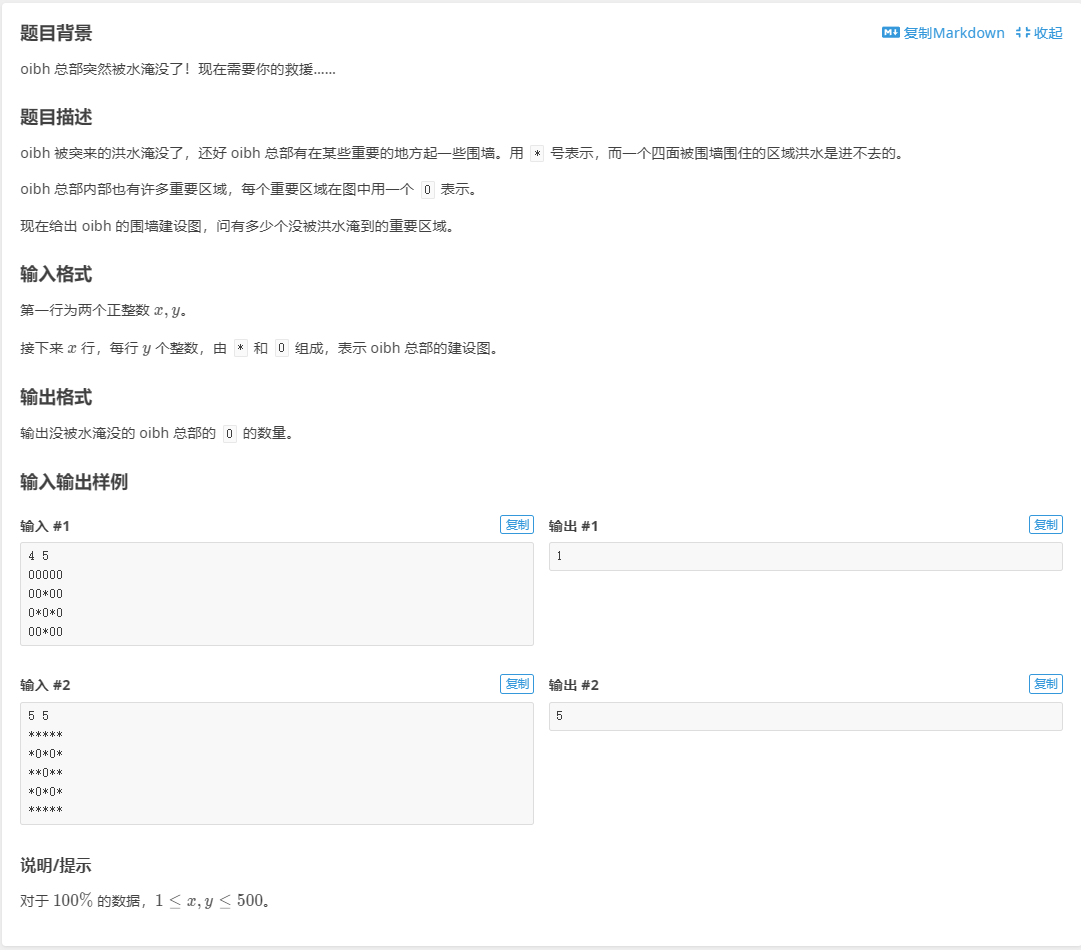如果你依然想套用上一题并信心满满的提交时,你会收到全WA的惊喜(我也一样233)其实我们可以在最外围搜一圈,凡是被洪水淹没的地段都设为1,最后循环查找没被淹没的地方(值为0的地方)就行了()
AC代码:
#include<stdio.h>
const int MAX = 510;
int arr[MAX][MAX], m, n, count = 0;
//方向数组
int ax[4] = {0, 0, 1, -1};
int ay[4] = {1, -1, 0, 0};
void dfs(int x, int y)
{
int x1, y1;
arr[x][y] = 1;
for (int i = 0; i < 4; i++)
{
x1 = x + ax[i];
y1 = y + ay[i];
if (x1 >= 0 && x1 < n && y1 >=0 && y1 < m && arr[x1][y1] == 0)
{
dfs(x1, y1);
}
}
}
int main(void)
{
//读入
scanf("%d%d\n", &n, &m);
for (int i = 0; i < n; i++)
{
for (int j = 0; j < m; j++)
{
char temp;
scanf("%c", &temp);
if (temp == '0')
{
arr[i][j] = 0;
}
else{
arr[i][j] = 1;
}
}
if (i != n - 1)
{
scanf("\n");
}
}
//在最外面一圈进行搜索
for (int i = 0; i < m; i++)
{
if (arr[0][i] == 0)
{
dfs(0, i);
}
if (arr[n - 1][i] == 0)
{
dfs(n - 1, i);
}
}
for (int i = 0; i < n; i++)
{
if (arr[i][0] == 0)
{
dfs(i, 0);
}
if (arr[i][m - 1] == 0)
{
dfs(i, m - 1);
}
}
//统计没有被淹没的地段
for (int i = 0; i < n; i++)
{
for (int j = 0; j < m; j++)
{
if (arr[i][j] == 0)
{
count++;
}
}
}
printf("%d", count);
}
P1036 [NOIP2002 普及组] 选数
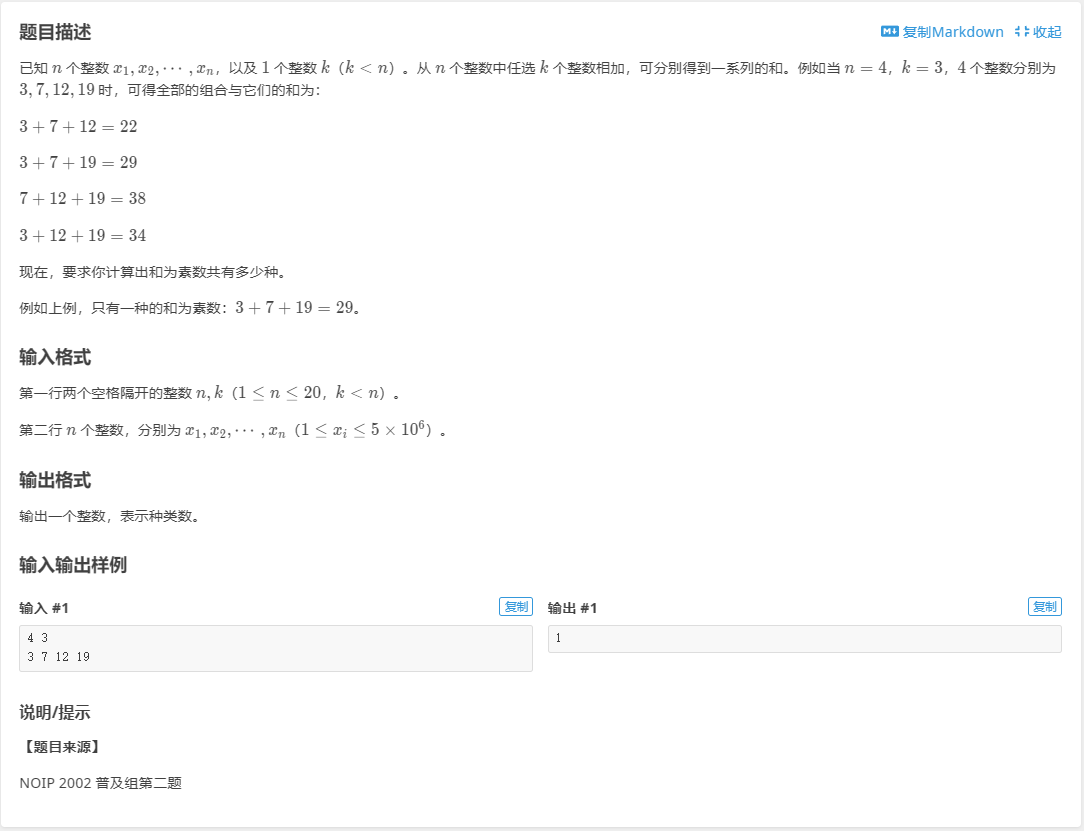此题跟其他dfs题如出一辙,可以说照着模版写就是了,唯一可能卡的点是判断是否为质数:int prime(int sum)
{
for (int i = 2; i * i <= sum; i++)
{
if (sum % i == 0)
{
return 0;
}
}
return 1;
}
dfs部分不作展示。
[USACO10OCT] Lake Counting S
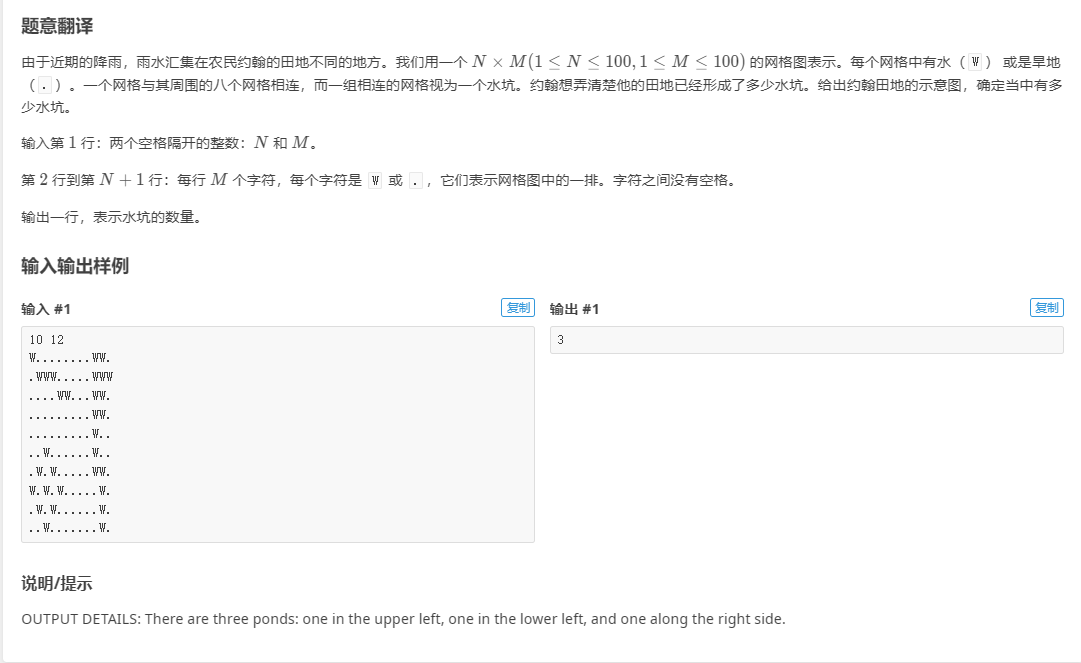也是一般dfs思路,唯一不同的地方在于为八个方向,只需要将方向数组修改就行了。 //东、东南、南、西南、西、西北、北、东北
int ax[9] = {0, 0, 1, 1, 1, 0, -1, -1, -1};
int ay[9] = {0, 1, 1, 0, -1, -1, -1, 0, 1};
dfs部分不作展示。
[USACO1.5] 八皇后 Checker Challenge
喜欢我八皇后吗,说实话,真的没一点思路。 在这个棋盘上,行列对角线上只能存在一个棋子,我写了点。
AC代码:
#include<stdio.h>
#include<math.h>
//分别对应行,主对角线,副对角线,答案数组。
int col[14], d1[30], d2[50], ans[14];
int n, w = 0;
void dfs(int x)
{
if (x > n)
{
//题只要求输出前3种情况,所以w<3,随后只让解的个数增加
if (w < 3)
{
for (int i = 1; i <= n; i++)
{
printf("%d ", ans[i]);
}
printf("\n");
}
w++;
}
else
{
for (int k = 1; k <= n; k++)
{
//平行的主对角线满足该特征:它们的行与列之差固定,但可能为负值,故再加上一个n。
int z = x + k - 1;
//平行的副对角线满足该特征:它们的行与列之和固定。
int t = x - k + n;
if (!col[k] && !d1[z] && !d2[t])
{
ans[x] = k;col[k] = 1;d1[z] = 1;d2[t] = 1;
dfs(x + 1);
col[k] = 0;d1[z] = 0;d2[t] = 0;
}
}
}
}
int main(void)
{
scanf("%d", &n);
dfs(1);
printf("%d", w);
}
P1189 SEARCH
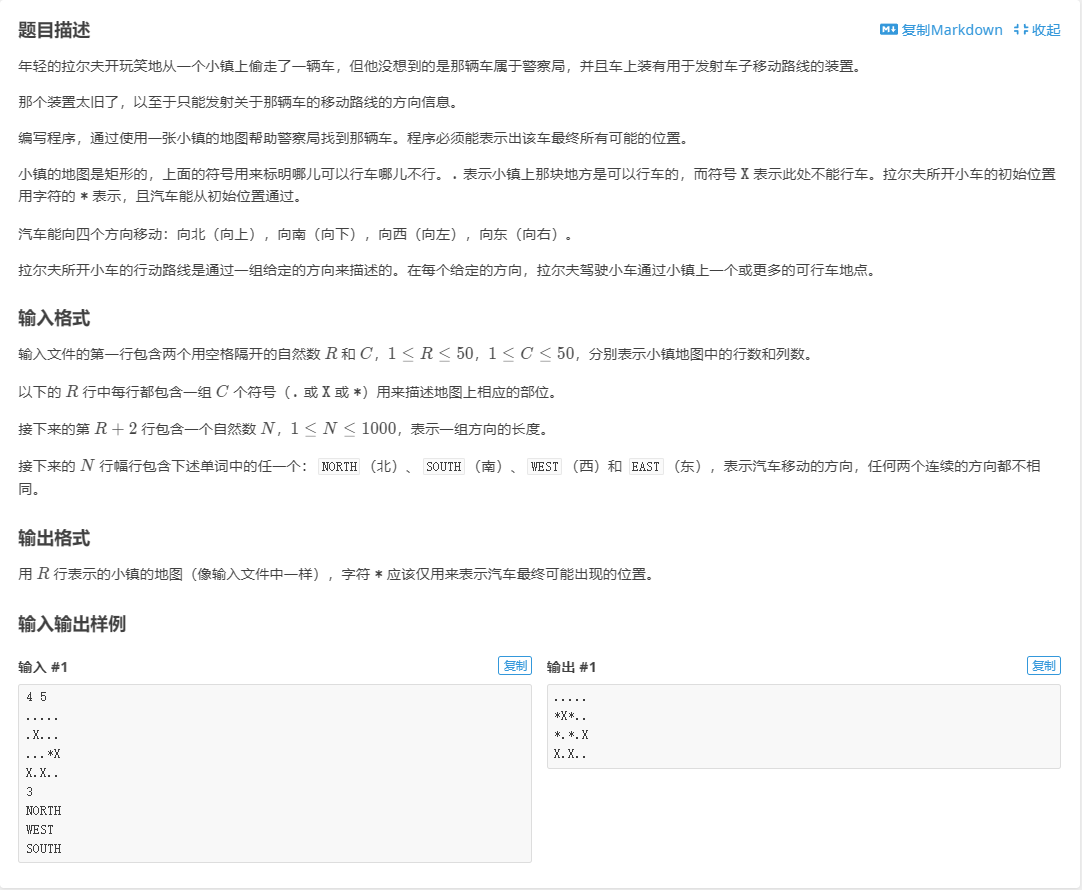这个题的意思是给你一个初始地与N个方向,N个方向都要按顺序使用,寻找到它最终的落脚点,这题DFS和BFS都可以用 参考：dingcx:P1189 SEARCH
考虑直接使用dfs会超时,我们选择优化,因为在dfs搜索过程中会出现多条路都通向一个节点的情况,我们在标记数组中加入方向长度减少这种情况,就进行优化,详细请读一读上面这篇文章~
AC代码:
#include<stdio.h>
const int MAX = 55;
const int MAXN = 1010;
int m, n, arr[MAX][MAX], arr1[MAXN][MAX][MAX], stx, sty, N, dir[MAXN];
int f[5][2] = {0,0,0,1,1,0,0,-1,-1,0};
void dfs(int len, int x, int y)
{
if (arr1[len][x][y] == 1)
{
return;
}
else
{
int x1 = x, y1 = y;
arr1[len][x][y] = 1;
if (len == 0)
{
return;
}
while (1)
{
x1 += f[dir[len]][0];
y1 += f[dir[len]][1];
if (arr[x1][y1] == 1 || x1 < 0 || x1 >= m || y1 < 0 || y1 >= n)
{
break;
}
dfs(len - 1, x1, y1);
}
}
}
int main(void)
{
scanf("%d%d\n", &m, &n);
for (int i = 0; i < m; i++)
{
for (int j = 0; j < n; j++)
{
char temp;
scanf("%c", &temp);
if (temp == 'X')
{
arr[i][j] = 1;
}
else if (temp == '.')
{
arr[i][j] = 0;
}
else{
stx = i;
sty = j;
arr[i][j] = 0;
}
}
if (i != m - 1)
{
scanf("\n");
}
}
scanf("%d\n", &N);
for (int i = 1; i <= N; i++)
{
char str[10];
scanf("%s", str);
if (str[0] == 'E')
{
dir[N + 1 - i] = 1;
}
else if (str[0] == 'S')
{
dir[N + 1 - i] = 2;
}
else if (str[0] == 'W')
{
dir[N + 1 - i] = 3;
}
else if (str[0] == 'N')
{
dir[N + 1 - i] = 4;
}
}
dfs(N, stx, sty);
for (int i = 0; i < m; i++)
{
for (int j = 0; j < n; j++)
{
if (arr1[0][i][j] == 1)
{
printf("*");
}
else if (arr[i][j] == 0)
{
printf(".");
}
else{
printf("X");
}
}
printf("\n");
}
}
春空舞う花びらは，
過ぎ去った奇跡じゃなく，
巡った季節を超えても輝いて，
二人の未来を彩るよ。